2016-12-04
https://leetcode.com/problems/combination-sum/
纯枚举。。。
2016-12-05
https://leetcode.com/problems/combination-sum-ii/
二分查找
2016-12-06
https://leetcode.com/problems/3sum/
三维降维到2维
2016-12-07
https://leetcode.com/problems/word-search/
图的搜索,要是先判断是不是要的单词,不是就跳过,再看旁边的单词,这为什么是DFS?
2016-12-08
https://leetcode.com/problems/summary-ranges/
纯遍历
2016-12-09
https://leetcode.com/problems/find-the-duplicate-number/
最佳方法: O(n) 时间复杂度 环检测 ,没做过肯定不会。
2016-12-12
https://leetcode.com/problems/next-permutation/
分类讨论
2016-12-13
https://leetcode.com/problems/set-matrix-zeroes/
拿数组自身的空间做标记
2016-12-15
https://leetcode.com/problems/first-missing-positive/
仍然是把数据存储在原本的空间
2016-12-16
https://leetcode.com/problems/spiral-matrix/
纯遍历
========================================================
- N皇后问题
递归: https://leetcode.com/submissions/detail/93563685/
非递归: https://leetcode.com/submissions/detail/93700718/
主/从对角线数量 2*n-1 主对角线 (左上右下) i+j恒定 从对角线 i-j+(n-1)
判断三种冲突情况 竖线冲突、主对角线冲突、从对角线冲突:
if (x == i || x+y == i+line || x-y == i-line) { break; }
- N个数的全排列
1. 用位操作方法:假设元素原本有:a,b,c三个,则1表示取该元素,0表示不取。以可以类似全真表一样,从值0到值2^n依次输出结果
2. 递归:从集合中依次选出每一个元素,作为排列的第一个元素,然后对剩余的元素进行全排列,如此递归处理
3. 非递归:只要对字符串反复求出下一个排列。由后向前找替换数和替换点,然后由后向前找第一个比替换数大的数与替换数交换,最后颠倒替换点后的所有数据
- 背包问题
- 士兵路径
- 桶排序
https://leetcode.com/problems/maximum-subarray/
- 作业题1
• 设计一个队列
• 支持:出队,入队,求最大元素
• 要求O(1)
• 均摊分析
https://gist.github.com/HsingPeng/1dbb6734db26f2e6c22424dd3ecbe5e0
参考https://ask.julyedu.com/question/7192
- 作业题2
• 给定一个正整数组a,是否能以3个数为边长构成三角形?
• 即是否存在不同的i,j,k,
• 满足 a[i] < a[j] + a[k]
• 并且 a[j] < a[i] + a[k]
• 并且 a[k] < a[i] + a[j]
http://m.weixindou.com/p/T7PV4X056EYKOB320ZM1.html
- 两个堆栈实现一个队列
- 直方图中最大长方体
https://leetcode.com/problems/largest-rectangle-in-histogram/
给定一个长度为n的直方图,我们可以在直方图高低不同的长方形之间画一个更大的长方形,求该长方形的最大面积。例如,给定下述直方图
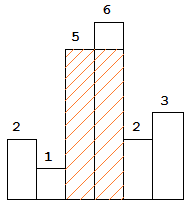
视频:七月在线 8月面试求职班 第7课 贪心
解法:计算每个方块的左右延伸最大长度,不降低高度,然后依次计算每个方块的高度值。
https://leetcode.com/submissions/detail/92383847/
估计我的算法200ms+超时,他的算法4ms,差距很大。
主要差距应该在比较左右高度时,我没有用数组记录之前测量过的值,每次都依次比较,造成很大冗余。他用
int L = i;
while (L > 0 && heights[L-1] >= heights[i]) {
L = left[L-1];
}
left[i] = L;
迅速跳过测量过的值。
关键思想:这个长方形的高肯定是某一个柱子的高,所以按柱子高来计算就行。
- 排列组合
算法之排列与组合算法
http://dongxicheng.org/structure/permutation-combination/
排列算法
- 字典序法 从最右开始,找到第一个比右边小的数字,交换
- 递归法 递归交换,最后一个数
组合算法 M N
- 递增进位制数法 二进制1表示保留,递增
- 01转换法 将数组前M个元素置1,从左扫描数组元素值的“10”变为“01”,同时将其左边的所有“1”全部移动到数组的最左端
==========================================
练习:
2017-6-12 15:14:00
快排
写了40分钟。。。。JAVA
2017-6-12 16:30:17
2017-6-12 16:34:26
堆排序
学习完毕,建堆,然后一个个抽走
2017-6-12 16:53:58
用最小堆
建堆过程有问题
看来建一个最大堆,输出的时候才能反过来是顺序排序。
2017-6-12 17:49:39
完成,一个小时。。。
2017-6-13 09:57:30
归并排序
2017-6-13 10:49:44
刚看了正则表达式,现在开始
2017-6-13 13:12:37
终于写好了,吃了个饭,日志有点事,然后算法写的有点问题,排错。
代码写的很烂,臃肿。改天再分析了。
2017-6-14 10:25:28
困,写个直接插入吧
2017-6-14 11:00:16
开始写,比较大小从后面向前依次比较
2017-6-14 11:08:40
博客里写的更优一点,它依次向后移动,然后把元素插入,我是每次都交换。
2017-7-18 21:18:27
写快排,思路
2017-7-18 21:54:20
开始写
2017-7-18 23:06:19
写完,全忘了,花了好长时间。
2017-7-19 20:58:44
今天还写个快排
2017-7-19 21:59:03
写完,还行,实际消耗半个小时。
2017-7-23 14:08:00
练习快排
2017-7-23 14:32:32
写完
2017-8-7 09:56:49
写个快排
2017-8-7 10:21:03
写完
==========================================
二叉树遍历,包括按层次遍历,先序、中序、后序遍历。
2017-8-7 11:49:21
编写
2017-8-7 14:00:16
编写
5
3 8
2 7 9
1 6
2017-8-9 17:49:54
这个遍历还有点难度,没写出来
前序 与 中序 后序 的非递归不同在于:
前序 访问顺序 中→左→右 导致 在入栈存储时,可以不存 中(根) 节点,只需要依次存储 右 左 节点。每个节点只会访问依次,不需要判断是否访问过。
而 中序 后序 则必须将 中(根)节点入栈,然后取出。
中序 是 左→中→右 ,则存储 中 节点,出栈时,取出 中 节点,这时 中(根)节点已经是第二次访问了,此时需要判断该节点是否是第二次访问,即是否遍历过其子节点。
第一次访问,读取其左节点;第二次访问,输出该节点并读取其右节点。
或者第一次访问,用于读取其左节点,并入栈 右 中 节点;第二次访问,用于输出该节点。
后序 是 左→右→中 ,则依次存储 中 右 节点,出栈时,右节点出栈,遍历其子节点。中(根) 节点出栈,输出该节点,这也是该节点的第二次访问了。与 中序 相同, 第一次,用于读取其左节点,第二次访问,输出该节点。
中序判断是否是第二次访问,可以通过判断上一个读取的节点是否为空。
第一次访问,上个读取的节点肯定等于当前节点。
后序判断是否是第二次访问,可以通过判断上一个读取的节点是否为空。
第一次访问,上个读取的节点肯定等于当前节点。
中序 非递归伪代码:
每个节点读取两次
stack.push(root);
p = root;
while (!stack.empty()) {
if (p != null) {
p = stack.peek();
p = p.left;
if (p != null) {
stack.push(p);
}
} else {
p = stack.pop();
visit(p);
p = p.right;
if (p != null) {
stack.push(p);
}
}
}
2017-8-10 22:12:55
验证正确
正常遍历一个节点会被读取三次,以后序为例:
第一次:读其左子节点
第二次:读其右子节点
第三次:读自己
若分三次读,而只有一个变量 p 来代表上次读取的节点,则:
p != null && p != 左 && p != 右 时(等同于 p == 自己),是第一次,此时 p == 自己,因为是父节点递归下来的
左 == null || p == 左 时,是第二次读
p == null || p == 右 时,代表第三次读,因为子节点读完才会回到自己。
后序遍历顺序 左→右→中,左 和 右 节点处理完p返回的都可能是null(都为空的情况下)。
因此读第一次时,依次将自己入栈,并且p = 左。左不存在则p = null。然后下一个循环。
栈顶的节点出栈,如果是 左 存在,则当前 p != null ,接着进入第一次读取 左 。
当 左 读完, p == 左 ,此时再出栈一个,肯定是其父节点 。满足第二次读取条件,右 入栈。
情况一 无 左 右:
第一次:输入 p == 自己 ,输出:p == null,自己在栈
第二次,输入 左 == null ,输出:p == null,自己在栈
第三次,输入 p == null ,输出:p = 自己,访问自己,出栈
情况二 无 右:
第一次:输入 p == 自己,输出:p == 左,自己在栈,左 入栈
间隔若干 左 里的调用
第二次:输入 p == 左 ,输出:p == null,自己在栈
第三次:输入 p == null,输出:p == 自己,访问自己,出栈
情况三 无 左:
第一次:输入 p == 自己,输出:p == null,自己在栈
第二次,输入 左 == null ,输出:p == 右,自己在栈,右 入栈
间隔若干 右 里的调用
第三次:输入 p ==右,输出:p == 自己,访问自己,出栈
情况四 有 左 右:
第一次:输入 p == 自己,输出:p == 左,自己在栈,左 入栈
间隔若干 左 里的调用
第二次,输入 p == 左 ,输出:p == 右,自己在栈,右 入栈
间隔若干 右 里的调用
第三次:输入 p ==右,输出:p == 自己,访问自己,出栈
后序 非递归伪代码:
每个节点读取三次
stack.push(root);
p = root;
q;
while(!stack.empty()) {
q = stack.peek();
if (p == q) {
p = p.left();
if (p != null) {
stack.push(p);
}
} else if (q.right != null && q.right != p) {
p = q.right;
if (p != null) {
stack.push(p);
}
} else {
p = stack.pop();
visit(p);
}
}
按照每个节点读取三次的思路 中序 非递归:
第一次:读其左子节点
第二次:读自己
第三次:读其右子节点
第二次读的条件是,读完了 左子节点,但是无法使用p变量来确定
中序 非递归:
stack.push(root);
p = root;
q;
while(!stack.empty()) {
q == stack.peek();
if (p == q) {
p = p.left();
if (p != null) {
stack.push(p);
}
} else if (无法确定) {
visit(p);
} else {
p = stack.pop();
p = p.right;
if (p != null) {
stack.push(p);
}
}
}
中序的第二次读和第三次读可以放一起处理,因为第二次读之后就是第三次读,没有间隔。
这样就可以处理了。
中序 非递归:
stack.push(root);
p = root;
q;
while(!stack.empty()) {
q == stack.peek();
if (p == q) {
p = p.left();
if (p != null) {
stack.push(p);
}
} else {
p = stack.pop();
visit(p);
p = p.right;
if (p != null) {
stack.push(p);
}
}
}
前序 非递归:
stack.push(root);
p = root;
q;
while(!stack.empty()) {
q == stack.peek();
if (p == q) {
visit(p);
p = p.left();
if (p != null) {
stack.push(p);
}
} else {
p = stack.pop();
p = p.right;
if (p != null) {
stack.push(p);
}
}
}
参考:二叉树遍历(先序、中序、后序)
http://www.jianshu.com/p/456af5480cee
整理:树的前序、中序、后序遍历(递归、非递归)
https://gist.github.com/HsingPeng/592db15b48753b177722541e201ff279
后序不同于中序、前序,多个第二次访问判断
} else if (top.getRight() != null && top.getRight() != lastVisit) {
其他流程完全一致,只是visit的点不一致。
2017-8-16 20:30:34
图的深度优先和广度优先搜索要看。

