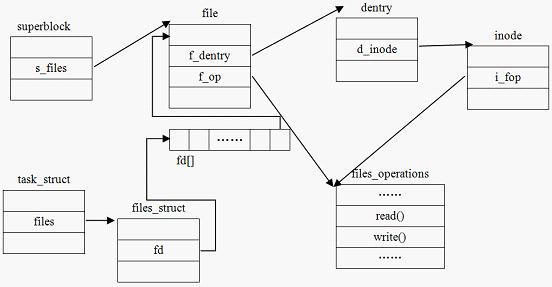
知识点
|
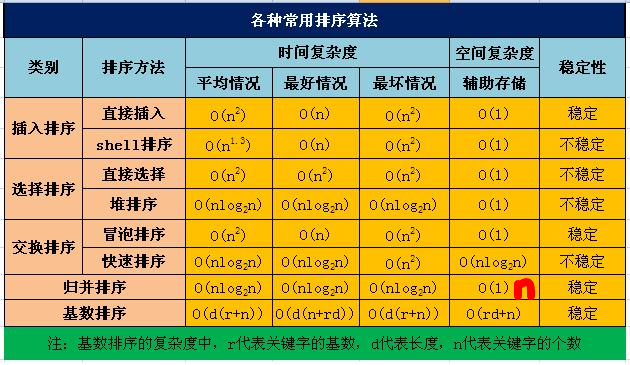
查找
|
平均时间复杂度
|
查找条件
|
算法描述
|
|
顺序查找
|
O(n)
|
无序或有序队列
|
按顺序比较每个元素，直到找到关键字为止
|
|
二分查找（折半查找）
|
O(logn)
|
有序数组
|
查找过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则搜素过程结束；如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较。 如果在某一步骤数组为空，则代表找不到。
|
|
二叉排序树查找
|
O(logn)
|
二叉排序树
|
在二叉查找树b中查找x的过程为：1. 若b是空树，则搜索失败2. 若x等于b的根节点的数据域之值，则查找成功；3. 若x小于b的根节点的数据域之值，则搜索左子树4. 查找右子树。
|
|
哈希表法（散列表）
|
O(1)
|
先创建哈希表（散列表）
|
根据键值方式(Key value)进行查找，通过散列函数，定位数据元素。
|
|
分块查找
|
O(logn)
|
无序或有序队列
|
将n个数据元素"按块有序"划分为m块（m ≤ n）。每一块中的结点不必有序，但块与块之间必须"按块有序"；即第1块中任一元素的关键字都必须小于第2块中任一元素的关键字；而第2块中任一元素又都必须小于第3块中的任一元素，……。然后使用二分查找及顺序查找。
|
1 直接插入排序：
2 希尔排序：
<span style="font-weight: bold;"--<
3 简单选择排序：
4 堆排序：
<span style="font-weight: bold;"--<
5 冒泡排序：
6 快速排序：
<span style="font-weight: bold;"--<
7 归并排序：
<span style="font-weight: bold;"--<
8 桶排序：
9 基数排序：
10 计数排序：
二分查找
二叉树遍历
归并排序参考 http://blog.csdn.net/morewindows/article/details/6678165/
八大排序参考 http://blog.csdn.net/hguisu/article/details/7776068
排序算法稳定性：定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，ri=rj，且ri在rj之前，而在排序后的序列中，ri仍在rj之前，则称这种排序算法是稳定的；否则称为不稳定的。
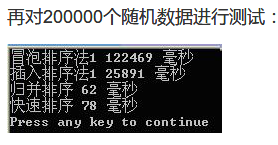
这效率，惊呆了
快速排序空间复杂度平均是O(NlogN)：http://harttle.com/2015/09/27/quick-sort.html
归并排序的空间复杂度是O(N):http://blog.csdn.net/yuzhihui_no1/article/details/44223225
归并排序在规模较大时比希尔和堆排序好；堆排序适合大数据；快排效率最高但大数据不行：http://blog.csdn.net/p10010/article/details/49557763
=====================================================
重点排序：
希尔排序 增量序列可取n/2
堆排序
快速排序
归并排序
代码示例： https://gist.github.com/HsingPeng/1980c786afd8c1a7fc169abdc4db66d6
堆：完全二叉树
二叉树
定义：二叉树是一个连通的无环图，并且每一个顶点的度不大于3
性质：
1 深度K的二叉树 最多2^k-1个节点
2 第i层的节点总数不超过 ,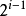
， i>=1
3 如果其叶结点数为N0，而度数为2的结点总数为N2，则N0=N2+1
4 有n个结点的完全二叉树的深度为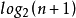
5 有N个结点的完全二叉树各结点如果用顺序方式存储：
若I为结点编号则 如果I>1，则其父结点的编号为I/2
如果2*I<=N，则其左儿子（即左子树的根结点）的编号为2*I；若2*I>N，则无左儿子；（从0计算：2*I +1）
如果2*I+1<=N，则其右儿子的结点编号为2*I+1；若2*I+1>N，则无右儿子。（从0计算：2*I +2）
6 给定N个节点，能构成h(N)种不同的二叉树。h(N)为卡特兰数的第N项。h(n)=C(2*n，n)/(n+1)。
卡特兰数？h(n) = h(1)*h(n-1) + h(2)*h(n-2) + ... + h(n-1)h(1)，n>=2
括号匹配问题
========================================================
2017-5-18 12:47:28
重点整理：
包括：基本思想、复杂度、优缺点、场景
重点排序：快排、堆排序、归并排序
排序示例代码：https://gist.github.com/HsingPeng/1980c786afd8c1a7fc169abdc4db66d6
树的遍历示例代码：https://gist.github.com/HsingPeng/592db15b48753b177722541e201ff279
1 快速排序：
基本思想：
选择一个基准元素，通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，
然后再按此方法对这两部分数据分别进行快速排序，
整个排序过程可以递归进行，以此达到整个数据变成有序序列。
复杂度：
平均O(n log n) 最好O(n log n) 最差n^2 空间O(n log n) 不稳定
优点：
目前基于比较的内部排序中被认为是最好的方法。
当待排序的关键字是随机分布时，快速排序的平均时间最短。
住快排一般情况下常数项小，复杂度相同但是消耗更小
缺点：
受基准元素影响大
时间复杂度不稳定，最差情况时间长。
场景：
一般情况或初始状态无序
2 堆排序：
基本思想：
堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。
堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。
从算法描述来看，堆排序需要两个过程，一是建立堆，二是堆顶与堆的最后一个元素交换位置。所以堆排序有两个函数组成。一是建堆的渗透函数，二是反复调用渗透函数实现排序的函数。
复杂度：
平均O(n log n) 最好O(n log n) 最差O(n log n) 空间O(1) 不稳定
优点：
排序速度稳定，不需要额外空间
数据量越大排序越快
缺点：
堆排序在建立堆和调整堆的过程中会产生比较大的开销
场景：
堆排序在建立堆和调整堆的过程中会产生比较大的开销，在元素少的时候并不适用。
但是，在元素比较多的情况下，还是不错的一个选择。尤其是在解决诸如“前n大的数”一类问题时，几乎是首选算法。
3 归并排序：
基本思想：
归并（Merge）排序法是将两个（或两个以上）有序表合并成一个新的有序表，即把待排序序列分为若干个子序列，每个子序列是有序的。然后再把有序子序列合并为整体有序序列。
复杂度：
平均O(n log n) 最好O(n log n) 最差O(n log n) 空间O(n log n) 稳定
优点：
归并排序是稳定的
缺点：
常数比快排略大，需要额外空间
场景：
大数据，外部排序
重点查找：二分查找、散列表、树（二叉树、B树、B+树、B*树、红黑树）
1 二分查找（线性表）
基本思想：
假设表中元素是按升序排列，将表中间位置记录的关键字与查找关键字比较，如果两者相等，则查找成功；否则利用中间位置记录将表分成前、后两个子表，如果中间位置记录的关键字大于查找关键字，则进一步查找前一子表，否则进一步查找后一子表。重复以上过程，直到找到满足条件的记录，使查找成功，或直到子表不存在为止，此时查找不成功。
复杂度：
最差O(log n)
优点：
比较次数少，查找速度快，平均性能好；
缺点：
要求待查表为有序表，且插入删除困难。
场景：
适用于不经常变动而查找频繁的有序列表。
2 散列表
基本思想：
散列表是根据关键码值(Key value)而直接进行访问的数据结构。它通过把关键码值映射到表中一个位置来访问记录，以加快查找的速度。
最关键的两点：哈希函数和冲突处理
冲突处理：
- 开放地址法 其基本思想是：当关键字key的哈希地址p=H（key）出现冲突时，以p为基础，产生另一个哈希地址p1，如果p1仍然冲突，再以p为基础，产生另一个哈希地址p2，…，直到找出一个不冲突的哈希地址pi
- 链地址法（拉链法） 将哈希地址相同的元素构成一个单链表
复杂度：
O(1)
优点：
实现了随机访问，所以性能比较快。
缺点：
当一个查找关键字对应多个散列地址；需要查找一个范围时（模糊查询），效果不好。
需要处理散列冲突。
散列冲突：不同的关键字经过散列函数的计算得到了相同的散列地址。
场景：
在海量数据处理中有着广泛应用
3 树
3.1 二叉查找树（BST树）
- 所有非叶子结点至多拥有两个儿子（Left和Right）；
- 所有结点存储一个关键字；
- 非叶子结点的左指针指向小于其关键字的子树，右指针指向大于其关键字的子树；
查找平均时间复杂度O(log n) 最坏情况退化成链表 O(n)
插入一个结点的代价与查找一个不存在的数据的代价完全相同，O(log n) 至 O(n)
删除时间复杂度，最少O(1)，最大不会超过O(logN)
3.2 平衡二叉搜索树（AVL树）
平衡二叉树或为空树,或为如下性质的二叉排序树:
- 左右子树深度之差的绝对值不超过1;
- 左右子树仍然为平衡二叉树.
查找时间复杂度保持在O(log n)
插入时间复杂度在O(logN)左右
删除时间复杂度O(2logN)
3.3 红黑树（RBT树）
红黑树是一种非严格平衡的二叉查找树
- 每个结点要么是红的，要么是黑的。
- 根结点是黑的。
- 每个叶结点（叶结点即指树尾端NIL指针或NULL结点）是黑的。
- 如果一个结点是红的，那么它的俩个儿子都是黑的。
- 对于任一结点而言，其到叶结点树尾端NIL指针的每一条路径都包含相同数目的黑结点。
含有n个节点的红黑树的高度至多为2*log(n+1)，它包含的内节点个数至少为2^(h/2)-1个。
红黑树能保证在最坏情况下，基本的动态几何操作的时间均为O(logn)
3.4 平衡多路查找树（B树、B-树、B~树）
一颗m阶的B树特性如下：
(1)树中每个节点最多含有m个孩子(m ≥ 2)；
(2)除根结点和叶节点外，其他每个节点至少有ceil(m/2)个孩子；
(3)根节点至少有两个孩子(除非B树只有一个节点-根节点)；
(4)所有叶节点出现在同一层，叶节点不包含任何关键字信息（每一个NULL指针即当做叶子结点）；
(5)每个非终端节点含有n个关键字，即(n,P0,K1,P1,K2,P2,...,Kn,Pn)。其中Ki(i = 1,2,...,n)为关键字,且关键字按顺序升序排列Ki-1且指针Pi-1指向子树中的所有节点的关键字均小于Ki且都大于Ki-1，关键字的个数n必须满足ceil(m/2)-1≤n≤m-1。比如,有j个孩子的非叶节点恰好有j-1个关键字。
3.5 B+树
一棵m阶的B+树和m阶的B树的异同点在于：
- 有n棵子树的结点中含有n个关键字； (有些资料上说与B 树n棵子树有n-1个关键字 保持一致，无关紧要，只是实现不同)
- 所有的叶子结点中包含了全部关键字的信息，及指向含有这些关键字记录的指针，且叶子结点本身依关键字的大小自小而大的顺序链接。 (而B 树的叶子节点并没有包括全部需要查找的信息)
- 所有的非终端结点可以看成是索引部分，结点中仅含有其子树根结点中最大（或最小）关键字。 (而B 树的非终节点也包含需要查找的有效信息)
B+树的磁盘读写代价更低
B+树的查询效率更稳定，支持基于范围的查询
3.6 B*树
在B+树的基础上(所有的叶子结点中包含了全部关键字的信息，及指向含有这些关键字记录的指针)，B*树中非根和非叶子结点再增加指向兄弟的指针；B*树定义了非叶子结点关键字个数至少为(2/3)*M，即块的最低使用率为2/3（代替B+树的1/2）。
B*树分配新结点的概率比B+树要低，空间使用率更高。
总结如下：
- B树：有序数组+平衡多叉树；
- B+树：有序数组链表+平衡多叉树；
- B*树：一棵丰满的B+树
- B树（二叉）：二叉树，每个结点只存储一个关键字，等于则命中，小于走左结点，大于走右结点；
- B-树：多路搜索树，每个结点存储M/2到M个关键字，非叶子结点存储指向关键字范围的子结点；所有关键字在整颗树中出现，且只出现一次，非叶子结点可以命中；
- B+树：在B-树基础上，为叶子结点增加链表指针，所有关键字都在叶子结点中出现，非叶子结点作为叶子结点的索引；B+树总是到叶子结点才命中；
- B*树：在B+树基础上，为非叶子结点也增加链表指针，将结点的最低利用率从1/2提高到2/3；
顺便说一句，无论是B树，还是B+树、b树，由于根或者树的上面几层被反复查询，所以这几块可以存在内存中，换言之，B树、B+树、B树的根结点和部分顶层数据在内存中，大部分下层数据在磁盘上。
其他：队列、栈、图
资料：
数据结构中常见的树（BST二叉搜索树、AVL平衡二叉树、RBT红黑树、B-树、B+树、B*树）
http://blog.csdn.net/sup_heaven/article/details/39313731
二叉查找树(BST)，平衡二叉查找树(AVL)，红黑树(RBT)，B~/B+树(B-tree）的比较
http://blog.csdn.net/bingjing12345/article/details/7830474
========================================================
有些概念：
分治、贪心、动态规划
动态规划
1 讲解
1.1 讲解1：七月在线--8月面试求职班
动态规划可以看成递归
动态规划 定义
• 原问题 -> 子问题 -> 原问题
• 最优子结构
• 子问题最优决策可导出原问题最优决策
• 无后效性
• 重叠子问题
• 去冗余
• 空间换时间
动态规划有两个非常重要的性质，最优子结构和重叠子问题。
动态规划就是去冗余
问题共性
• 套路
• 最优，最大，最小，最长，计数
• 离散问题
• 容易设计状态（整数01背包问题）
• 最优子结构
• N-1可以推导出N
直观的理解，只考虑整数，不考虑小数，就是离散。
题目的状态规模是有限制的
基本步骤
• 四个步骤
• 设计暴力算法，找到冗余
• 设计并存储状态（一维，二维，三维数组）
• 递归式（状态转移方程）
• 自底向上计算最优解（编程方式）
实例：
https://leetcode.com/problems/house-robber
斐波那契数列
N！
小兵向前冲
01背包问题
最长公共子序列
1.2 讲解2：《编程之法》
动态规划一般用来求解最优化问题，其适用条件是要求待求解的最优化问题具备两个因素：最优子结构和子问题重叠。通过求解一个个最优子问题，将解存入一张表中，当后续子问题的求解需要用到之前子问题的解时直接查表，每次查表的代价为常数时间。
与贪心法的区别：
贪心法是特殊的动态规划（子问题不重叠），贪心法是“最优子结构且局部最优”，动态规划是“最优独立重叠子结构且全局最优”
求解过程关键：
- 状态的定义
- 方案的枚举（仅枚举必要的）
- 最优子问题（一个状态的最优值取决于达到这个状态的全部子状态最优值） 和无后效性保证（状态之间的最优值不互相影响）
- 子问题有重叠
- 编写状态转移方程（当前节点的值完全由其前驱结点确定）
实例：
最大连续乘积子数组
从N个整数中找了(n-1)个元素乘积最大的那一组
字符串编辑距离
格子取数问题
交替字符串
1.3 讲解3：《剑指Offer》第二版
如果能够把小问题的最优解组合起来能够得到整个问题的最优解，就可以用动态规划。
特点1：求一个问题的最优解
特点2：整体问题的最优解是依赖各个子问题的最优解
特点3：小问题之间还有相互重叠的更小的子问题
特点4：从上往下分析问题，从下往上求解问题
贪婪算法和动态规划不一样，贪婪的每一步都能确定是最优解。
所以应用贪婪时，需要用数学方式证明贪婪选择是正确的。
实例：
剪绳子（第二版）
连续子数组的最大和（第一版）
2 问题举例
2.1 问题一：连续子数组的最大和 《剑指Offer》第二版
/**
* 连续子数组的最大和
*
* 方法一：数组规律
* @param array
* @return
*/
public static int maxSubString(int[] array) {
int max = Integer.MIN_VALUE;
int last = 0;
for (int p : array) {
if (last >= 0) {
last = last + p;
} else {
last = p;
}
if (max < last) {
max = last;
}
}
return max;
}
/**
* 连续子数组的最大和
*
* 方法二：动态规划
* @param array
* @return
*/
public static int maxSubString1(int[] array) {
int max = Integer.MIN_VALUE;
int last = 0;
for (int p : array) {
last = Math.max(p, last + p);
max = Math.max(max, last);
}
return max;
}
2.2 问题二：最大连续乘积子数组 《编程之法》
/**
* 最大连续乘积子数组
*
* 比如：{-2.5, 4, 0, 3, 0.5, 8, -1} 最大连续是 3 0.5 8
*
* @param array
* @return
*/
public static double maxSubProduct(double[] array) {
double max = array[0];
double lastMin = array[0];
double lastMax = array[0];
for (int i = 1 ; i < array.length ; i++) {
double current = array[i];
lastMin = Math.min(Math.min(current * lastMin, current * lastMax), current);
lastMax = Math.max(Math.max(current * lastMax, current * lastMin), current);
if (lastMax > max) {
max = lastMax;
}
}
return max;
}
2.3 问题三：最长递增子序列（LIS）
最长递增子序列 O(NlogN)算法
https://www.felix021.com/blog/read.php?1587
nlogn
最长递增子序列
https://github.com/julycoding/The-Art-Of-Programming-By-July/blob/master/ebook/zh/05.06.md
n^2
/**
* 最长递增子序列
*
* 比如：
* {2, 1, 4, 3, 1, 5, 6} 返回： 4
* [157,232,6] 返回 2
* @param A
* @return
*/
public static int findLongest(int[] A) {
int max = 0;
int[] last = new int[A.length];
last[0] = 1;
for (int i=1 ; i<A.length ; i++) {
int current = 0;
for (int j=0 ; j<i ; j++) {
int temp = 0;
if (A[j] < A[i]) {
temp = last[j] + 1;
} else {
temp = 1;
}
if (temp > current) {
current = temp;
}
}
last[i] = current;
if (max < last[i]) {
max = last[i];
}
}
return max;
}
2.4 问题四：分装粉笔 360 2018 秋招笔试
小明一共有n根彩色粉笔，m根白色粉笔，
现在可以用a根彩色粉笔和b根白色粉笔组成一盒卖x元，
或者c根白色粉笔组成一盒卖y元，或
者d根彩色粉笔组成一盒卖z元，
小明最多可以用这些粉笔卖多少元？不一定要把粉笔卖完，小明只希望利益最大化。
输入：
n m
a b c d
x y z
输入样例：
5 15
1 2 3 6
2 1 3
输出样例：
11
========================================================
